इस पोस्ट में हम गति के तीन समीकरणों की व्युत्पत्ति (Derivation of Equations of Motion) की विधि पर चर्चा करेंगे (for class 9 motion chapter)। गति के समीकरण समय के संबंध में इसकी गति के (in terms of its motion with respect to time) संदर्भ में एक भौतिक प्रणाली के व्यवहार का वर्णन करें । ये समीकरण हैं केवल तभी मान्य होता है जब त्वरण स्थिर या एकसमान हो (uniform acceleration or constant acceleration)।
**You can also check this Related Post on motion numericals/संबंधित पोस्ट: Motion Numerical problems for class 9
Table Of Contents
- गति का पहला समीकरण (वेग-समय संबंध के लिए समीकरण) व्युत्पत्ति | First Equation of Motion (Equation for velocity-time relation) derivation
- गति का दूसरा समीकरण (स्थिति-समय संबंध या दूरी-समय संबंध के लिए समीकरण) व्युत्पत्ति | derivation of the Second Equation of Motion (Equation for position-time relation or distance-time relation)
- गति का तीसरा समीकरण (स्थिति-वेग संबंध या दूरी-वेग संबंध के लिए समीकरण) व्युत्पत्ति | Third Equation of Motion (equation for position-velocity relation or distance-velocity relation) derivation
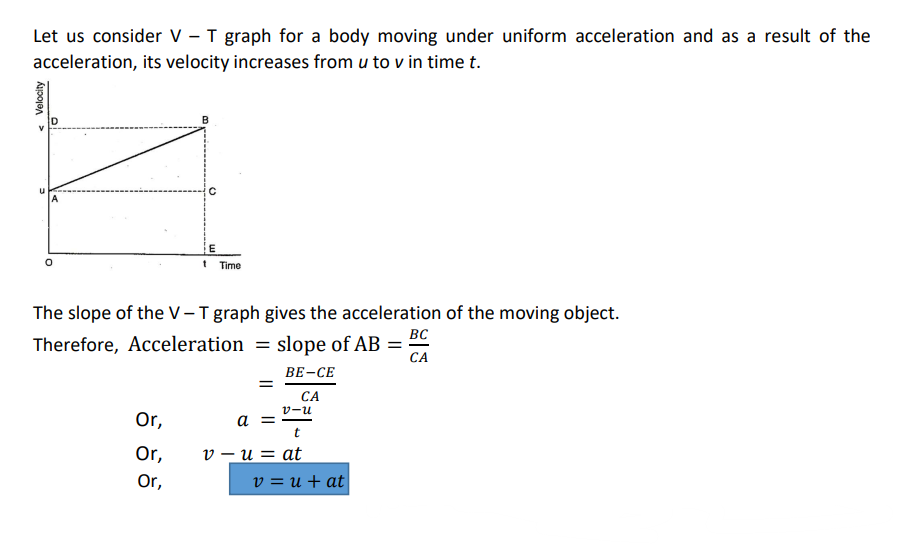
गति का पहला समीकरण (वेग-समय संबंध के लिए समीकरण) व्युत्पत्ति | First Equation of Motion (Equation for velocity-time relation) derivation
Derivation of the equation: 𝑣 = 𝑢 + 𝑎𝑡
गति का दूसरा समीकरण (स्थिति-समय संबंध या दूरी-समय संबंध के लिए समीकरण) व्युत्पत्ति | derivation of the Second Equation of Motion (Equation for position-time relation or distance-time relation)
Derivation of the equation: s = ut + (1/2)at2

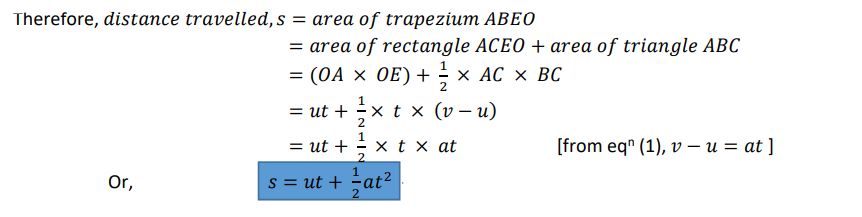
गति का तीसरा समीकरण (स्थिति-वेग संबंध या दूरी-वेग संबंध के लिए समीकरण) व्युत्पत्ति | Third Equation of Motion (equation for position-velocity relation or distance-velocity relation) derivation
Derivation of the equation: v2 = u2 + 2as

