प्रक्षेप्य गति पराबोलिक है, इसे सिद्ध कीजिए [projectile motion is parabolic – prove it (class 11)]
यहां हम यह सिद्ध करेंगे कि प्रक्षेप्य गति पराबोलिक होती है। इसे सिद्ध करने के लिए हमें प्रक्षेप्य पथ समीकरण (Projectile Motion Path Equation or Projectile trajectory equation) को derive करना होगा। (कक्षा 11)
प्रक्षेप्य गति पराबोलिक है (कक्षा 11) – चलिए यह सिद्ध करें | projectile motion is parabolic – prove this
मान लीजिए कि कोई वस्तु समान वेग V0 से क्षैतिज (X) अक्ष के साथ θ कोण बनाते हुए फेंकी जाती है।
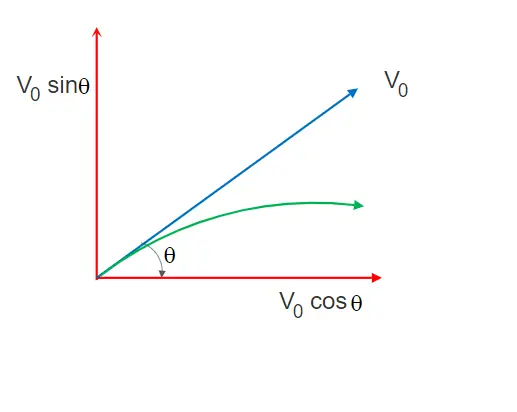
चित्र में, हम प्रारंभिक वेग V0 और इसके X तथा Y अक्षों के साथ resolved components को प्रक्षेप्य गति के लिए दर्शा रहे हैं (समय t = 0 पर वेग के components)
क्षैतिज X-अक्ष के साथ आरंभिक वेग का component = V0x = V0 cosθ
और ऊर्ध्वाधर Y-अक्ष के साथ आरंभिक वेग का component = V0y = V0 Sinθ
(वायु प्रतिरोध को अनदेखा किया गया है)
समय T = 0 पर, X और Y अक्षों के साथ कोई विस्थापन नहीं है।
समय T=t पर, (अर्थात् किसी भी समयावधि t के लिए) X-अक्ष के साथ विस्थापन = x = V0x.t = (V0 cosθ). t………… (1)
और Y-अक्ष के साथ विस्थापन = y = (V0 sinθ).t – (1/2) g t2…………(2)
समीकरण 1 से हम प्राप्त करते हैं: t = x/(V0 cosθ)………….. (3)
समीकरण 2 में t को समीकरण 3 से प्राप्त t के अभिव्यक्ति से प्रतिस्थापित करते हैं:
y = (V0 sinθ). x/(V0 cosθ) – (1/2) g [x/(V0 cosθ)]2 या, y = (tanθ) x – (1/2) g. x2/(V0 cosθ)2………..(4)
उपर्युक्त समीकरण में g, θ, और V0 constant हैं।
*आइए समीकरण 4 को पुन: लिखें: y = ax + bx2 , जहाँ a और b constant हैं। यह एक पराबोला का प्रतिनिधित्व करने वाला समीकरण है।
इस प्रकार, हम कह सकते हैं कि प्रक्षेप्य का पथ या गतिपथ एक पराबोला है। और, प्रक्षेप्य गति पराबोलिक होती है। इस प्रकार, किसी कोण (लंबवत् कोण को छोड़कर) पर फेंकने पर, प्रक्षेप्य एक वक्र पथ पराबोला का अनुसरण करेगा।
