Last updated on June 16th, 2023 at 12:52 pm
धारा का वहन करने वाले तार के लूप को किसी एकसमान चुंबकीय क्षेत्रा B में रखा गया है। यह किसी नेट बल का अनुभव नहीं करता। परंतु इस पर एक बल–आघूर्ण (torque) क्रिया करता है। इस बल–आघूर्ण की प्रवृत्ति पाश को घूर्णित कर इसवेफ समतल को, क्षेत्रा की दिशा के अनुलंब लाने की होती है। इसी सिद्धांत के आधार पर सभी विद्युत मोटर तथा मीटर आदि कार्य करते हैं।
We will find out the formula of the Torque on a Current Loop in Hindi (धारा लूप पर बल-आघूर्ण)
Torque on a Current Loop in Hindi | धारा लूप पर बल-आघूर्ण
यदि लूप का समतल चुंबकीय क्षेत्रा के अनुलंब हो तो उस पर न तो कोई नेट बल और ना ही कोई बल आघूर्ण होगा।
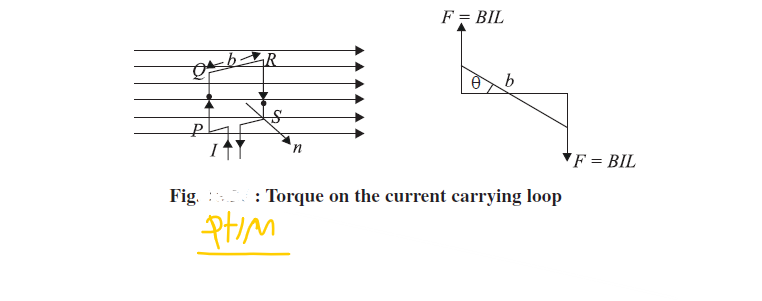
बल आघूर्ण = बल × बल के मध्य लांबिक दूरी = B IL. b sin θ
चित्रा का अवलोकन करें जिसमें धरा I को वहन करने वाला लूप PQRS दर्शाया गया है। चुंबकीय क्षेत्रा B और कुंडली के समतल के अभिलंब n के मध्य कोण θ है।
तब, बल आघूर्ण,
τ = NBIL b sin θ
जबकि N कुंडली पर turns की संख्या है। हम पुनः निम्नलिखित रूप में लिख सकते हैः
|τ| = NBI A sin θ
जबकि A कुंडली का क्षेत्रफल = L x b
Formula of the torque on a current loop kept in a magnetic field | बल-आघूर्ण formula in Hindi
|τ| = |B| |M| sin θ
जबकि M = NIA है जो धरा वाहक कुंडली का चुंबकीय आघूर्ण [magnetic moment of the current carrying coil ] कहलाता है। इस प्रकार हम देखते हैं कि बल–आघूर्ण [Torque] B,A,I,N तथा θ पर निर्भर करता है।
Magnetic Moment formula | चुंबकीय आघूर्ण फार्मूला | magnetic dipole moment formula
धारा वाहक कुंडली का चुंबकीय आघूर्ण का फार्मूला [formula of magnetic moment of the current carrying coil]
M = NIA
N कुंडली पर turns की संख्या है
I = current [धारा]
A = कुंडली का क्षेत्रफल
Numerical problem for practice (with solution link)
1] 8 cm त्रिज्या और 30 turns की कोई वृत्ताकार कुंडली 6.0 A की धारा का वहन कर रही है। यह वुंफडली 1 T के एकसमान क्षैतिज चुंबकीय क्षेत्रा में निलंबित है। क्षेत्रा रेखाएं, कुंडली के अभिलंब के साथ 90 डिग्री का कोण बनाती हैं। कुंडली को मुड़ने से रोकने के लिए लगाए गए प्रति बल–आघूर्ण के परिमाण को परिकलित कीजिए।
Summary
A loop of current-carrying wire placed in a uniform magnetic field (B) experiences no net force but a torque acts on it. This torque tends to rotate the loop to bring its plane perpendicular to the field direction. This is the principle that underlines the operation of all electric motors, meters, etc.
|τ| = |B| |M| sin θ
where M = NIA is known as the magnetic moment of the current-carrying coil.
Thus, we see that the torque depends on B, A, I, N and θ
